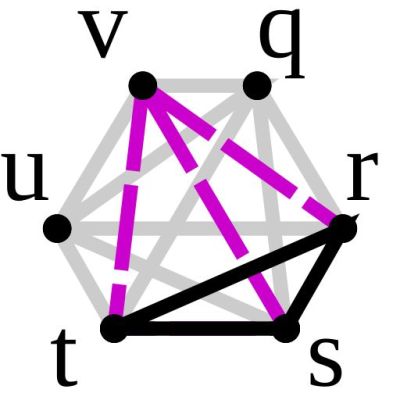
Generally when assuming a chaotic (i.e. random) system like an undirected graph, we assume that if we start coloring these (i.e. assign values) with two colors no real pattern emerges. Yet it’s been proven that if you have a graph with a certain set of vertices, coloring the resulting lines in this manner will always result in a clique forming. This phenomenon has been investigated for nearly a century now after its discovery by British mathematician [Frank P. Ramsey].

The initial discovery concerned a graph with 6 vertices, providing the lowest number of vertices required. Formally this is written as R(3, 3), with subsequent cases of these Ramsey numbers discovered. They are part of Ramsey theory, which concerns itself with the question of what the underlying properties are that cause this apparent order to appear, which requires us to discover more cases.

Finding the number for a particular instance of R(m, n) can be done the traditional way, or brute-forcing it computationally. Over the decades more advanced algorithms have been developed to help with the search, and people from different fields are mingling as they are drawn to this problem. So far the pay-off of this search are these algorithms, the friendships created and perhaps one day a deep insight in the causes behind this phenomenon that may have implications for physics, chemistry and other fields.